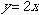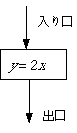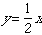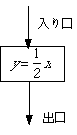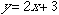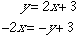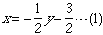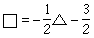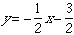逆関数せつめい器
「逆関数せつめい器」というのは、ほぼ正方形の厚紙の表と裏に、フェルトペンで下のような
図を書いたものです。
これは、逆関数のグラフの様子を説明するのに使う道具ですが、事前に逆関数とはどういうものかをきちんと話しておかないと、誤解が生じかねません。
1. 逆関数とは
中学で習ったように、関数とは「入り口と出口のある箱」です。例えば
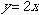 | では、どこが入り口でどこが出口ですか? |
というような問いかけで、xが入り口を表す文字、yが出口を表す文字であることを確認しておきます。
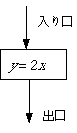
上の図で、入り口に例えば1,2,3を入れると、出口からそれぞれ2,4,6が出てきます。逆関数とは上の箱でやった仕事を元に戻すような仕事をする箱のことです。
| いまの場合は逆関数は明らかに | 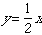 | です。 |
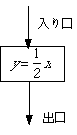
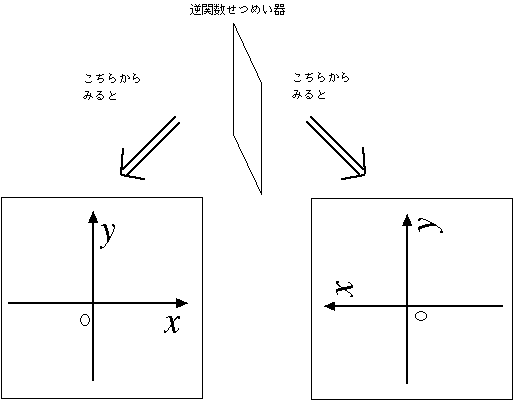
| では、次に | 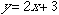 | の逆関数をもとめてみましょう。 |
「xが入り口を表す文字、yが出口を表す文字」なので、この式は
「(出口)= 」という形をしています。そこで逆関数を求めるには、式を変形
して、「(入り口)= 」すなわち「x= 」という形にします。
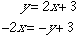
両辺を−2で割ると
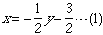
(1)より逆関数は
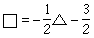
という形をしていることがわかります。「入り口を表す文字をx、出口を表す文字をy」とするので、逆関数は
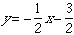
です。
以上のことから、大づかみに言うと、
「もとの関数の入り口と出口を入れ替えたのが逆関数だから、逆関数をつくるには入り口を表す文字xと出口を表す文字yを入れ替えればよい」という
ことができます。
2. 逆関数のグラフ
それでは逆関数のグラフはどうなっているのでしょうか。1.でわかったことより、
逆関数のグラフはもとの関数のグラフのx軸とy軸を入れ替えたものになっている
ということが予想できます。
ここでいよいよこのページの主役の登場です。似ていないのを承知の上で一生懸命ドラえもんの真似をして「逆関数せつめい器〜」と叫びながら、例の厚紙を取り出します。下の写真のように持って、
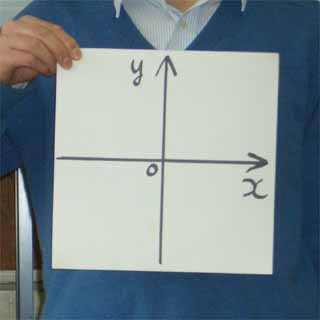
「このx軸とy軸を入れ替えるには、厚紙を
どういうふうに動かせばいいのだろうか」ときいてみます。全体を左に90°回転すると、x軸はもとのy軸のところに来ますが、y軸はもとのx軸と反対向きになってしまいます。同じように、全体を右に90°回転してもうまくいきません。生徒もなかなか気がつかないようです。最後は「こうするんだよ」と言いながら、せつめい器の右上と左下をもってぐるっと裏返します。
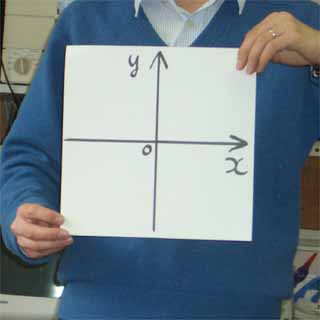



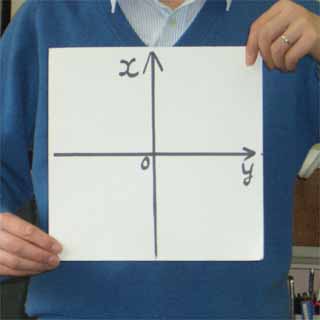
安価な材料ですぐできますが、結構インパクトのある道具です。