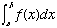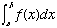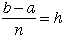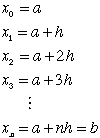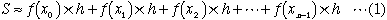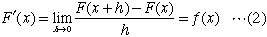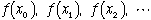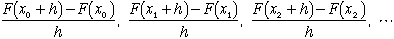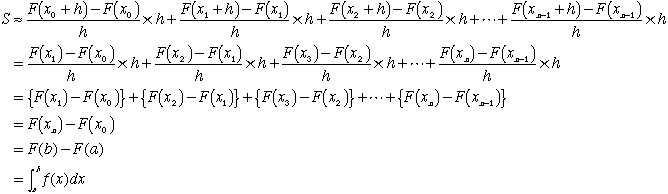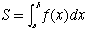定積分が面積を表すわけ
関数f(x)はa≦x≦bで「連続かつf(x)>0」とします。このとき、定積分
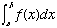
は、「y=f(x)のグラフとx軸および2直線x=a,x=bで囲まれた」下図の斜線部の面積Sを表します。
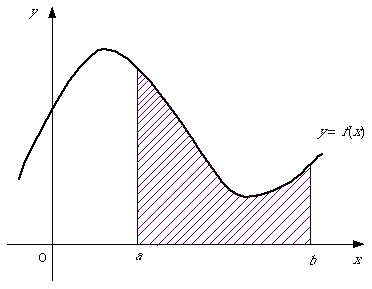
図1
(理由)
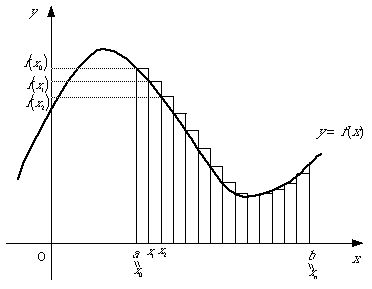
図2
区間[a,b]をx0,x1,x2,x3,・・・,xnにn等分する。
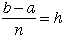 | とすると |
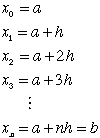
nを大きな数にすれば、図1の斜線部の面積Sは、図 2の細長い長方形の面積の和で近似できます。
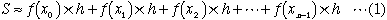
いまf(x)の不定積分の一つをF(x)とすると
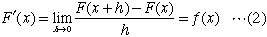
nが大きな数のとき、hは0に近い数になるので、(2)より、(1)の
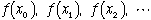 | は | 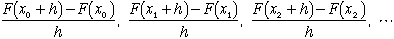 | で近似できます。 |
すると
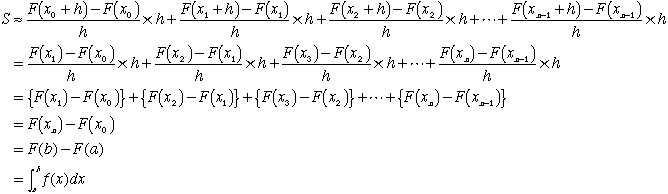
nを限りなく大きくすれば
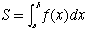
となります。