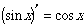サインのグラフをシートで調べる
正方形の薄い透明プラスチック板に、白の油性フェルトペンで対角線を1本書いた
下の写真のようなシートを使って、サインやコサインのグラフの様子を調べてみま
しょう。

このシートの上と下の端をくっつけて円筒状にしたものを横からはなれて見ると
サインやコサインのグラフが現れます。理由はすぐおわかりでしょう。

ここで重要なことはこれが縦横の比率まで正確なグラフだということです。
シートの1辺の長さを2πとすれば、円柱の底面の直径は2、高さは2πになる
からです。現在の数IIでは、旧課程で数IIIに移った弧度法が復活していますが、このシートを用いれば、ラジアン単位できちんとかかれたサインやコサインのグラフのようすを知ることができます。
更にシートを使って、サインやコサインのグラフが横軸と交わるときの角度が
45°であることまで、次のようにしてわかってしまいます。
まず、黒板にチョークで斜め45°の直線を書き、その上にこのシートを重ねます。
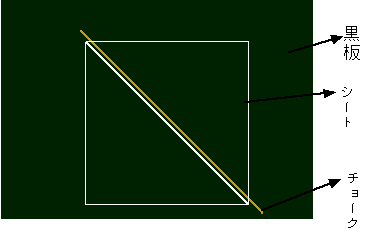
次にシートの上と下を手前に持ってきて円筒状にします。するとこのとき、いちばん奥側の、黒板とシートが接しているところだけが変わっていないので、ここの角度は45°のままのはずです。
また、このシートを使って、サインの導関数を求めることもできます。
シートを円筒状にすれば、さっきと同じ理由で、いちばん手前の角度0に相当する
部分は傾きが1ですので、下のように、直角二等辺の三角定規を当てると、
斜辺とグラフは接しています。

ここで、全体を角xだけ回転すると、横から
はなれて見たとき、三角定規の横の辺の長さは変わりませんが、縦の辺は
斜めになるのでcosx倍に見えます。

よって接線の傾きはcosxで、
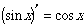
であることがわかります。