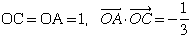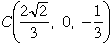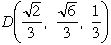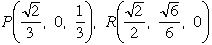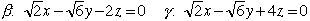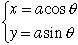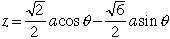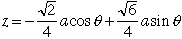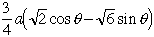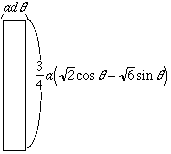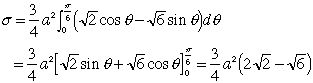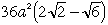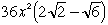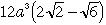2.の答
(1)『互いに直交する2本(あるいは3本)の直線を軸とする半径aの2個(あるいは3個)
の円柱の共通部分の体積』
のような問題でも、この問題でも、考えている立体図形の表面は、いずれかの円柱のいくつかの部分が集まったものになります。
更に、このような問題で軸l,m,.n,…の円柱の共通部分をWとすると、Wの表面とlを軸とする円柱とが一致するのは「軸lからの距離が、他のどの軸m,.n,…からの距離よりも遠くなるような領域」であることがわかります。
(2)次に、立方体ABCD-EFGHを考え、その中心をOとします。すると、4点ACFHを頂点とする四面体は正四面体となることから、今回の問題は
『AG,BH,CE,DFを軸とする半径aの4本の円柱の共通部分の体積を求める。』
としても良いことがわかります。
(3)そこで(1)より、「軸AGからの距離が、他の3本のどの軸からの距離よりも遠くなるような領域」を求めてみることにします。
(4)まず、軸AGからの距離のほうが軸BHからの距離よりも大きくなるような領域から考えてみます。AGからの距離とBHからの距離が等しくなるのは、「AGとBHのなす角の二等分線を含んでしかも、AGとBHを含む平面に垂直な平面」上の点であり、このような平面は2つあります。1つは、立方体の2つの面、ADFEとBCGFのどちらとも平行で2つの面から等距離にあるような平面、もう1つは4つの頂点CDEFを含むような平面です。この2枚の平面によって空間は4つの部分に分かれますが、これらのうち、軸BHが通っている2つの部分を合わせた領域が、「軸AGからの距離のほうが軸BHからの距離よりも大きくなるような領域」です。白い紙を折って立方体を作り、いま求めた領域に入っているところを色のサインペンで塗ってみてください。
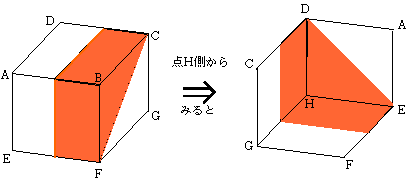
(5)続いて「(軸AGからの距離)>(軸CEからの距離)となる領域」、
「(軸AGからの距離)>(軸DFからの距離)となる領域」もそれぞれ違う色のサインペンで、立方体を塗ってください。3つの色が重なった領域が、「軸AGからの距離が、他の3本のどの軸からの距離よりも遠くなるような領域」です。これは下の図の青い部分になります。
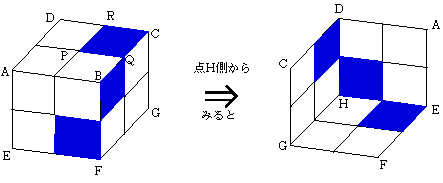
(6)立方体ABCD-EFGHの各面を向かい合う辺の中点どうしを結んで
「田の字」形に分けると全部で24個の小正方形になります。
「軸AGからの距離が、他の3本のどの軸からの距離よりも遠くなるような領域」は、
Oから見た立体的な方向がこの24個のうちの上の図の6個の青い小正方形の方向になる
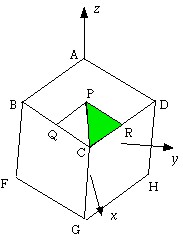
ことがわかりました。(1)で考えたことより、この領域では、いま問題にしている立体図形の表面は、AGを軸とする円柱と一致します。同様に、Oから見た立体的な方向が24個のうちの別の6個の小方形の方向では、「問題の立体の表面が、BHを軸とする円柱と一致」します。更にOから見て「問題の立体の表面が、CEを軸とする円柱と一致」する方向、「問題の立体の表面が、DFを軸とする円柱と一致」についても全く同じことが言えます。いま、3点OPCを含む平面をα、OPRを含む平面をβ、OCRを含む平面をγ( ただしP,Rは上の図のような点)、また「AGを軸とする半径aの円柱(の側面)を3つの平面α、β、γで切った部分(のうち最小のもの)の面積」をσとします。対称性を考慮すれば、σの48倍が求める立体図形の表面積になります。
(7)空間座標を使ってσを求めてみましょう。立方体は方向を示すためだけに用いていて、大きさは関係ないので、Oを原点、A(0,0,1)とします。点Cがxz平面内におさまり、点Cのx座標が正になるようにx軸の向きを定めると、正四面体の性質より
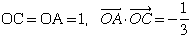
であるので
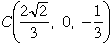
点FはCをz軸のまわりに−120°回転した点、点DはFとOに関して点対称な点なので
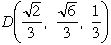
これらから
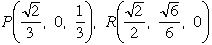
平面βとγの方程式は、法線ベクトルが図形的にすぐ求めることができるので容易にわかり
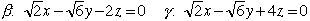
一方、AGを軸とする半径aの円柱の方程式は
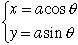
これを平面の方程式へ代入することより
βと円柱の交線では
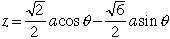
γと円柱の交線では
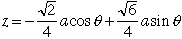
以上より、円柱(の側面)上でのz座標の差は
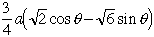
θとθ+dθに挟まれた微小部分は下のような長方形で近似できるので
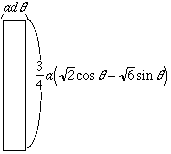
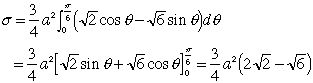
(8)これより問題の立体図形の表面積は
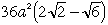
ところで、円柱の半径が微小量hだけ増えると、この立体の体積は(表面積)×hだけ増えます。この性質は、今回の問題の立体だけでなく、(1)で考えたような立体すべてで成り立っています。そこで、問題の立体の体積は
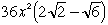
をxについて0からaまで積分すればよく、
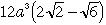
であることがわかりました。
数学の問題ページへ
先頭ページへ