mを2以上の整数とする。このとき、
を満たす自然数の組(p,q)が、どんなmに対しても少なくとも4つ存在することを示せ。 |
mを2以上の整数とする。このとき、
を満たす自然数の組(p,q)が、どんなmに対しても少なくとも4つ存在することを示せ。 |
mを2以上の整数とする。このとき、
を満たす自然数の組(p,q)が、どんなmに対しても少なくとも4つ存在する。…(*) |
(定義A)
|
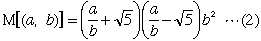
| ここで | 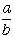 | が | 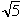 | のある程度良い近似値ならば | 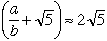 | でほぼ一定なので、 |
| 「 | 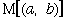 | の絶対値が小さい」ということは、 | 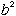 | と | 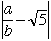 | の積が小さいことを表すと考えられます。 |
| いま | 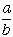 | と | 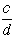 | を | 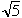 | の近似値とすると | 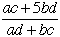 | は更に良い近似値となります |
| (特に | 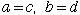 | のときがニュートン法の漸化式に相当します)。 |
(定義B)
|
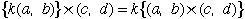
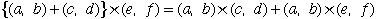
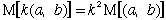
|
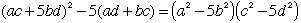
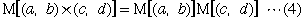
( 補題)
(証明終) |
| [1]自然数対の列 | 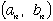 | を |
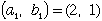
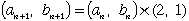
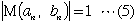
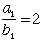 | と( 補題)より、すべてのnについて |
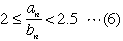
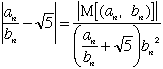
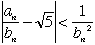
| これより | 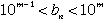 | のとき | 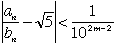 | となるので、 |
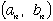 | は問題の(p, q)の条件を満たします。そして |
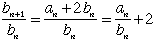 | と(6)より | 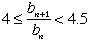 | なので |
| どの2以上の自然数mについても | 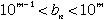 | をみたす | 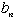 | は必ず1つまたは2つあります。 |
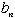 | と | 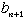 | の2つある場合には | 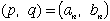 | と | 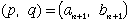 | の2組の解が得られます。 |
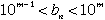 | をみたす | 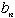 | が1つしかない場合は必ず | 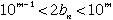 | であるので、 |
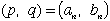 | と | 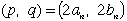 | で2組の解を得ることができます。 | <
| [2]別の自然数対の列 | 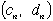 | を |
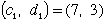
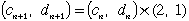
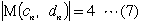
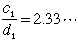 | と( 補題)より、すべてのnについて |
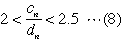
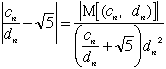
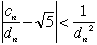
| 前の場合と同様にして、 | 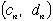 | は問題の(p, q)の条件を満たします。そして | 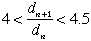 | より、 |
| 全ての2以上の自然数mについて | 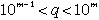 | を満たす解(p, q)として、 |
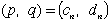 | と | 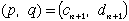 | の形の2組、または |
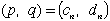 | と | 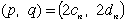 | の形の2組 |
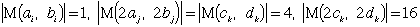
| かつ | 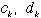 | はともに奇数なので、 |
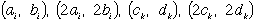 | のどの2つをとっても等しくなることはありません。 |
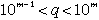 | かつ | 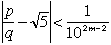 |